FEATURE: Taking the guesswork out of quality control

Conventional wisdom says that manufacturing engineers should aim for zero defects but, in reality, that’s often just too expensive.

In practice, engineers often have to make gut decisions about what’s ‘good enough’. 

With the new scientific approach to quality engineering, this type of guesswork is no longer required. Optimisation algorithms can select production processes and inspection instruments that will maximise profit. They can also decide when to reject products, based on their probability of non-conformance, and the potential cost implications of passing non-conforming products to the customer. 

This approach yields the most profitable production system possible for a given product, taking the guesswork out of quality engineering.

A cost-optimised approach to quality has been described by Professor Alistair Forbes, leader of the data science group at the National Physical Laboratory (NPL). His ideas were described in his 2006 paper “Measurement uncertainty and optimised conformance assessment,” published in the journal Measurement.

In both the conventional and state-of-the-art methods, statistical assumptions are made. The variation in production, and the uncertainty of verification measurements, are assumed to follow some identifiable probability distribution. Often this is the normal, or Gaussian, distribution. This means that statistics such as the mean and the standard deviation, of a sample of parts, can be used to estimate the non-conformance rate. 

Another way of looking at this is to determine the probability that a randomly chosen part will be non-conforming. For example, approximately 99.7% of parts produced will be within ±3 standard deviations, often described as 3-sigma. The number of standard deviations is also sometimes referred to as the z-score.

The current approach

In conventional quality engineering, ‘process capability’ is given in terms of the ratio between the product tolerance and the process accuracy (Cpk) or variation (Cp). This may also be expressed as the percentage of non-conforming parts that the process is expected to produce. A Cpk of 1.33, equating to a 0.0063% non-conformance rate, is commonly deemed the minimum value for a capable process. If it is assumed that all of these non-conformances will be detected by the quality control system, then it is easy to evaluate the cost of different non-conformance rates in terms of scrap. 

However, the cost of achieving a 0.0063% non-conformance rate often cannot be justified in terms of scrap alone. There is always some chance that non-conforming product will reach the customer. This may incur significant additional costs and, perhaps, provides justification for a zero-defects approach.

A similar approach is taken to deciding whether measurements are capable of detecting non-conforming parts. Conventionally, it is recommended that the accuracy of the measurement is less than 1/10 the tolerance being checked. In practice, this is often very difficult to achieve and the VDA-5 standard deems an expanded uncertainty that is less than 30% of the tolerance to be capable.

A great deal of time may be spent designing experiments and performing analysis on the data to understand the variation in production processes and the uncertainty of measurements. However, deciding what action should be taken based on the resulting data often comes down to the experience and intuition of a production engineer.

Making data-driven decisions

Key decisions for quality engineering include: which instruments and production processes to select; when to recalibrate them; and when to reject or rework products that appear to be non-conforming. Ideally, quality engineering should be able to use process variation and measurement uncertainty data to make these decisions in a mathematically optimal way. In general, an optimal decision is one that maximises the profitability of the production system. When considered in such a way, the one-size-fits-all approach of aiming for ‘capability’ does not make sense.

“In the context of conformance assessment in manufacturing, value is realised by making better decisions about the fitness-for-purpose of a component,” writes Forbes of the NPL. “The challenge is to use the available measurement data effectively in order to arrive at the best decisions, taking into account the fact that the data will have associated uncertainties. 

“Because of the uncertainties, no matter how good our decision-making procedure is, we will make a wrong decision from time to time, incurring a cost, a decision cost. Improving the quality of our data should (if our decision-making procedure is valid) reduce decision costs, but at the expense of increasing the cost of acquiring the improved data.”

In the box on page 39, two fictitious examples of products are used. These have been chosen deliberately to illustrate the point that different levels of capability are required for different products.

The first example is a shoe. In this case, the cost implication of a non-conforming product reaching the customer is relatively small. Should the customer experience a problem with their shoe, as a result of the non-conformance, they can be reimbursed easily. A friendly customer service representative, supplying them with two new pairs of shoes, would more than compensate them for the inconvenience. Their brand loyalty would be fully restored. The maximum cost of non-conformance is, in this case, relatively small. It may, therefore, be economical to reduce production and inspection costs, allowing non-conforming products to occasionally reach customers.

The second example is a fastening for a parachute harness. Should a non-conforming product reach the customer, there would be a significant probability of a fatal accident. It is assumed that the fastening is produced by a small business. Being implicated in a fatality would result in the bankruptcy of this business. In this case, significant resources should be invested in reducing production variation and measurement uncertainty. This should ensure that there is a very small probability of a defect ever reaching a customer.

Even for the shoe example, it would not be optimal if most of the products sold were non-conforming. At the other extreme, it would not be possible to reduce to zero the probability of a non-conforming parachute being used. Both examples have some optimum level which must be uniquely determined. The latest quality engineering methods are able to identify this optimal level.

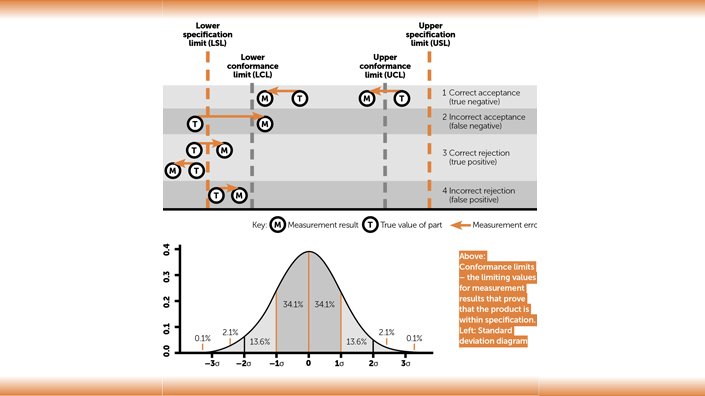
Understanding conformance limits

To understand optimisation of quality, it is first necessary to understand the distinction between a conformance limit and a specification. The specification, or tolerance, gives the actual design limits for the product. If the specification is met then the product will perform as intended. Conformance limits are the limiting values for measurement results that prove that the product is within specification. If it were possible to measure with zero uncertainty then the conformance limits would be equal to the specification limits. 

However, if a real measurement result is very close to the specification limit, then it is possible that the product is out of specification, but, owing to a small error in the measurement system, it appears to be within specification. To avoid passing defective products in this way, it is normal to reduce the specification limits by the uncertainty of measurement, to give conformance limits that prove conformance. 

The distance between the specification limits and the conformance limits may be expressed as a z-score, multiplied by the standard deviation of the measurement. This indicates the confidence at which conformance is proven.

There are four possible outcomes when a part is measured:

1 The true value of the part is within the specification limits and the measurement result is within the conformance limits. It is therefore correctly accepted by quality control (QC). This is also known as a true negative, since the result of the test for non-conformance is negative.

2 The true value of the part is outside the specification limits but the measurement result is within the conformance limits. So it is incorrectly accepted by QC, known as a false negative. This is the only outcome where a defect reaches the customer.

3 The true value of the part is outside the specification limits and the measurement result is outside the conformance limits. It is therefore correctly rejected by QC, also known as a true positive.

4 The true value of the part is within the specification limits but the measurement result is outside the conformance limits. It is therefore incorrectly rejected by QC, also known as a false positive.

Such a consideration leads to a number of trade-offs, which it is difficult to quantitatively resolve using a conventional approach. For example, increasing the confidence at which conformance is proven involves setting conformance limits further from the specification limits. This reduces the incorrect acceptance rate but also increases the incorrect rejection rate. Fewer defects reach the customer, but more parts are scrapped, many of which were not actually defective. 

Another trade-off is that if production capability is very high then very few parts will approach the conformance limits. Therefore, if the process is very capable, the measurement does not need to be so capable. The inverse is also true: a highly capable measurement reduces the need for a capable process somewhat.

Calculating quality-adjusted cost

An expected cost is simply the cost if an event occurs, multiplied by the probability that it will occur. This concept is well established in management accounting. It can also be used to evaluate the profitability of a production system, as the quality-adjusted cost per product sold. To calculate this, two conditional probabilities are required:

P₁ is the probability of a product being produced within the specification and then correctly passing quality control, the correct acceptance rate.

P₂ is the probability of a product being produced out of specification but then incorrectly passing quality control, the false acceptance rate.

The probability of a randomly chosen product conforming to its specification depends only on the accuracy of the production process. However, the probability of a product conforming and then being correctly passed by quality control depends on the accuracy of the production process, the uncertainty of the inspection measurement, and where conformance limits are set. This type of conditional probability is commonly used in Bayesian statistics. It is not easy to calculate by hand, but can be calculated in an instant using widely available algorithms.

If C₁ is the actual cost of producing and inspecting a product, then cost per product sold to the customer is given by C₁/(P₁+P₂). There is, however, another cost that must be considered. C₂ is the expected cost of passing a defective product to the customer, due to potential liability or loss of reputation. This cost only occurs when a defective product passes quality control, therefore C₂ is multiplied by P₂ to give its expected cost per part produced. 

Putting this together gives a simple equation for the quality-adjusted cost, C_Q, per part reaching the customer: 

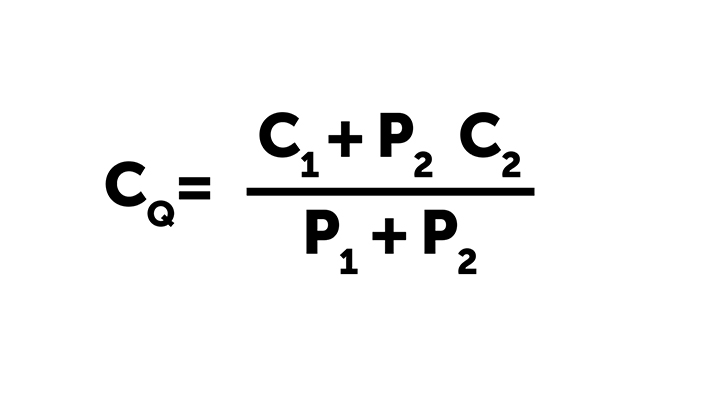
The objective, when planning a production system, is to minimise this cost.

Optimising conformance limits

Using the quality-adjusted cost, the optimum confidence level for conformance limits can be determined. Assuming the production process and inspection system are already known, the production cost, C₁, is therefore also known. C₂ may be estimated, considering the implications of defects reaching the customer. It is advisable to use worst-case estimates here. 

The quality-adjusted cost therefore depends on the probabilities of products reaching the customer that are conforming (P₁) and non-conforming (P₂). These probabilities depend on where conformance limits are set. It is, therefore, possible to calculate the quality-adjusted cost for a number of conformance limits and plot a curve to intuitively determine the optimum, corresponding to the minimum cost. In practice, a binary search algorithm may be used to find the optimum, in place of a graphical plot.

When the distance between the conformance limits and the specification limits is half the tolerance, the conformance limits touch each other and 100% of parts are rejected. The cost per part accepted therefore becomes infinite. This is, therefore, the upper limit to the optimisation curve. 

At the other end of the curve, the confidence level for accepting parts is too low and defects reach the customer, increasing the cost of quality (P₂C₂). The quality-adjusted cost curve therefore curves upwards at both ends. 

“Optimised conformance assessment uses statistics and optimisation to achieve the balance between the measurement and decision costs that maximises the expected value gain,” says Forbes.

Selecting production and inspection processes

Let us now take a step back and assume that the production process and inspection system have not yet been selected. The production system optimisation now starts by creating a list of possible production processes, together with their associated costs and expected accuracies. Similarly, potential measurement systems would be listed, together with their cost and expected uncertainty. 

The potential configurations for the system are therefore all of the possible combinations of production process and measurement system. An optimisation of conformance limits can be carried out for each combination, to obtain the minimum possible quality-adjusted cost for each. The final step is therefore to simply select the combination of production process and inspection system with the lowest cost.

Optimising production

This methodology can be best understood by considering two simplified examples, the shoe and the parachute. Only one production process will be considered for each product, with two measurement systems to be selected from in each case.

Step forward: making shoes

The specified tolerance is ±0.5mm for the interface between layers of the sole. If this interface is out of specification there is a 20% chance that the shoe will fail in use. The cost to fully compensate the customer in such an event is £20, giving C₂ = 20% x £20 = £4.

The production process has a standard deviation of 0.15mm, giving C_PK = 1.11 which would generally not be considered capable. The production cost is £3. Two measurement systems are being considered:

1. A coordinate measuring machine (CMM) with an expanded uncertainty of 0.17mm. At 28% of the tolerance, this would typically be accepted. Using the CMM it costs £0.35 to inspect each shoe.

2. A visual inspection process has an expanded uncertainty of 0.4mm, which is 80% of the tolerance, definitely not capable according to conventional guidelines. Using this process it only costs £0.02 to inspect each shoe.

When conditional probabilities are calculated these show that in either case approximately 1 in 10¹¹ defects actually reach the customer. Regardless of the measurement process selected, optimal conformance limits are set on the specification limits, at z = 0. Using the CMM the quality-adjusted cost per shoe is £3.35 and using the visual inspection it is £3.02. The scrap and defects reaching customers add no significant cost. It would, therefore, be optimal to select the visual inspection process, despite it being apparently not capable.

Landing safely: making a parachute fastening

The tolerance is ±0.2mm and if the part is out of tolerance there is a 10% chance of failure. A single failure is expected to result in bankruptcy with a cost of £4m (C₂ = £400,000). The production process has a standard deviation of 0.14mm, giving a C_PK of only 0.48, definitely not ‘capable’. The production cost is £5. Two measurement systems are being considered:

1. CMM-1 has a standard uncertainty of 0.14mm, 70% of the tolerance, so would not be considered capable. Inspection cost is £0.35.

2. CMM-2 has a standard uncertainty of 0.014mm, 7% of the tolerance, so is very capable. Inspection cost is £0.68.

Optimally, conformance limits should be set at z = 4.1, much higher than would normally be recommended. Using CMM-1 the quality-adjusted cost is £7.72 and using CMM-2 it is £5.73. In this case the capable instrument would be selected. The less-capable instrument would produce significant scrap costs as well as an unacceptable risk to the customer.

Many quality engineers are still applying a one-size-fits-all approach developed in the 1930s. But by applying a cost-optimised quality approach, considerably more profitable production systems are possible.